Table of Contents
Imaginary number i
\[i^2=-1\]
\[x^2=-1\]
\[x=i \lor x=-i\]
Equation degree and number of solutions
- Every n degree equation has n solutions
\[x^4=1\]
\[(x^2-1)(x^2+1)=0\]
\[x=1 \lor x=-1 \lor x=i \lor x=-i\]
Complex plane
- Complex numbers are those that have a real (x-axis) and an imaginary (y-axis) part, usually called z
Imaginary unit circle

- Numbers in the imaginary unit circle have a modulus, distance, r of 1
- \(z=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i\)
- \(r=\|z\|=\sqrt{\left(\frac{1}{\sqrt{2}}\right)^2+\left(\frac{1}{\sqrt{2}}\right)^2}=1\)
Addition
- \((a+bi)+(c+di)=(a+c)+(b+d)i\)
Conjugates
- \(\bar{z}=a-bi\) (mirror on the x-axis)
- \(z+\bar{z}=a\)
- \(z\cdot\bar{z}=\|z\|^2\)
- \(\overline{z+w}=\bar{z}+\bar{w}\)
- \(\overline{zw}=\bar{z}\bar{w}\)
- \(\overline{z^n}=\bar{z}^n\)
Angle
- Also called \(\theta\), argument of z or arg(z)
- It can be calculated from a and b (x and y coordinates), between \(-\pi\) and \(\pi\) :

- \(\tan{\theta}=\frac{y}{x}\)
- \(arg(\frac{1}{z}) = -r\)
- \(arg(-z) = arg(z) + \pi\)
- \(arg(\bar{z})=-arg(z)\)
- for z * w we are adding the angles (arguments) of the complex numbers
- The length of the new number is the product of their respectives moduluses
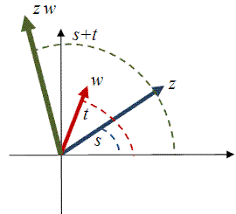
- \(\|z\cdot w\|=\|z\|\|w\|\)
- \(\arg(z+w)=\arg(z)+arg(w)\)
- This can be directly expressed in polar form
- \(z=r(\cos{\theta}+i\sin{\theta})\)
Eulers identity
- \(z=r(\cos{\theta}+i\sin{\theta})=re^{i\theta}\)
- \(zw=\|z\|\|w\|(\cos{(s+t)}+i\sin{(s+t)})=\|z\|\|w\|e^{i(s+t)}\)
- \(z\cdot\bar{z}=\|z\|^2\)
- Because we have \(\theta + -\theta\), therefore a real, positive number
- z and its conjugate have the same length, therefore the length squared
- \(\frac{z}{w}=\frac{\|z\|}{\|w\|}(\cos{(s-t)}+i\sin{(s-t)})=\frac{\|z\|}{\|w\|}e^{i(s-t)}\) (for s \(s\neq 0\))
- \(z^n=\|z\|^n(\cos{(n\theta)}+i\sin{(n\theta)})=\|z\|^ne^{in\theta}\)
- Re(zw) = Re(z)Re(w) – Im(z)Im(w)
- Im(zw) = Re(z)Im(w) + Im(z)Re(w)


